How to Always Boot Mac OS X in Verbose Mode
![]() Booting Mac OS X as usual shows the Apple logo and eventually you’ll wind up at a login screen or desktop, that’s attractive and all, but some users would prefer to see what’s going on behind the scenes. That’s what Verbose Boot Mode does, it shows you what is really happening during system startup on a Mac, and is great for troubleshooting purposes, but it can also just be interesting to see what exactly is going on during the MacOS and Mac OS X booting process.
Booting Mac OS X as usual shows the Apple logo and eventually you’ll wind up at a login screen or desktop, that’s attractive and all, but some users would prefer to see what’s going on behind the scenes. That’s what Verbose Boot Mode does, it shows you what is really happening during system startup on a Mac, and is great for troubleshooting purposes, but it can also just be interesting to see what exactly is going on during the MacOS and Mac OS X booting process.
Typically, if you wanted to boot in verbose mode on a per boot basis you would hit Command-V during startup, which brings up the familiar white on black console looking screen with a lot of scrolling text. On the other hand, some users may prefer to always see the complete verbose booting process on every boot including all kernel extension loading, details, and system messages on boot, and to do that you can adjust the firmware from the Terminal with the nvram command, as we’ll cover here.
How to Turn On Always Verbose Booting for Mac OS X
Simply execute the following nvram command at the Terminal to enable verbose boot mode and set it to ‘always’ (meaning every system boot is verbose by default):
sudo nvram boot-args="-v"
Disabling Verbose Booting on the Mac
Equally simple is the ability to disable verbose booting, which will basically make Mac OS X boot as normal – this is the default boot behavior of every Mac:
sudo nvram boot-args=
Check current nvram firmware boot settings
If you’re curious what the current firmware nvram settings are, type the following:
nvram -p
That will show you the current nvram parameters, indicating if something like verbose mode or safe boot is enabled, but you’ll also see some other data there too that may appear as gibberish – for our purposes here you can ignore all that and just focus on the boot arguments.
What is Verbose Boot Mode on Mac?
Verbose boot mode is helpful when troubleshooting your Mac, particularly when used in conjunction with Mac OS X safe booting. It allows you to see everything your Mac is doing on system boot, so if there is an error thrown or something going wrong during the system boot process, it’s easier to identify. It’s a text only boot mode, but it will be exited from automatically when the Mac OS X boot process has completed enough to enter into the graphical user interface. This is what it looks like roughly to boot Mac OS X with verbose option enabled:
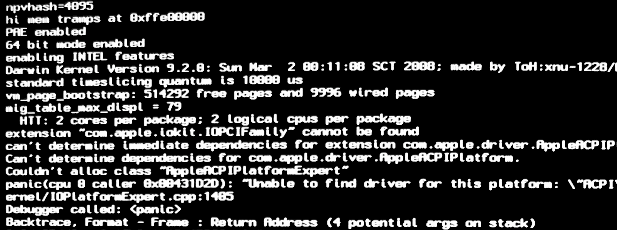
Most users will have no need to boot verbose, unless out of curiosity, or performing some particularly complex troubleshooting or diagnostics tasks on a Mac. Nonetheless, it can be an interesting trick to see what’s going on, and in many ways it resembles looking at a Terminal screen or booting a Linux PC as the kernel details scroll by during the loading process.


Verbose Mode is not supported as a permanent setting on Apple Silicon Macs due to changes in the boot process.
I used these instructions to set up the Mac to start verbose and have had no issues with software or anything else. I can tell better how the start-up is progressing rather than the non-descript “blank” apple screen with it’s misleading progress bar.
I tried the Verbose boot and now sorry that i did because some of my applications had to be re-authorized which is a huge pain in the studio ( polite way of saying it ) . There was no warning of that happening in this article unless I completely missed reading that warning or heads-up information.
So what i learned is to never do the Verbose boot .
I have this on but now it wont let me do
sudo dtrace -w -n “BEGIN{ panic();}
How do i do that command now?
I want to reset my password in verbose mode. How can i do it?
[…] Always boot Mac OS X in Verbose Mode sudo nvram boot-args=”-v” and to remove: sudo nvram boot-args= (tags: OSX Unix tutorial) […]
Just download Onyx for either Tiger or the newer version for Leopard +. There is a box to choose which mode you want it to start up in. WARNING… Not recommend to start up in single mode. Also for you Mac lovers that don’t want Spotlight to index anymore there is a box to un-check also in Onyx. So much easier than hacking up your registry.
[…] Verbose mode can be useful when troubleshooting Macs and developers often use it too. The standard user probably has no need to be in verbose, but it can still be fun to look at the underpinnings of Mac OS X. If you just hold down the key combination, your next reboot will be normal again, but you can also set your Mac to always boot in verbose mode. […]
ok i type -v NOT -V does that matter?
after some scrolling text the screen goes black but my PC is still running cause it has the light on and i can here it like usually. whats going on here?
Just what I needed. Thanks!
[…] MIGHT be it: Always boot Mac OS X in Verbose Mode – OS X Daily […]
could i use this command to reset the PRAM from first boot, as i understand it, setting something like
sudo nvram boot-args=”-p -r”
should reset the PRAM, and then would allow the system to boot normally( as the command would wipe its self out)
why i ask?
my mini no longer lets me reset PRAM from either a wired, or a wireless keyboard.(target disk mode works, option boot wont)
but all keys work fine once the OS is booted. :( any help please!
-w
Much too late for you, but maybe someone else will find this useful…
I have run into this many times. It seems like certain Macs (generally older Intels and most PPCs) simply will not take the PRAM reset key combination (command+option+p+r) or recognize an “option boot” from anything but the Apple white + clear plastic keyboard. The Aluminum keyboards just won’t do this on these machines.
When correcting others’ grammatical errors, please be sure that your response is correct. Americans is a proper noun so it should be capitalized.
When correcting grammatical errors in corrections to others’ grammatical errors, please be sure your response to their response is correct. “Americans” should be quoted.
When correcting grammatical errors in corrections to other’ grammatical errors in a reply that was supposed to correct errors in another reply, … Oh, I give up.
When correcting grammatical errors in corrections to others’ grammatical errors in a reply that was supposed to correct errors in another reply, one must have a correction in mind.
This must be an apple thing lol
A statistic:
Only 1 in 10 dumb americans can spell “definItely” correctly.
I just use a speel chkr
I definitely use a spell checker to check my spells, don’t like them to backfire, but I’m really good at spelling so I don’t need a spelling checker. Aluminium doesn’t need to be capitalized except at the beginning of a sentence.
hi. i have a macbook laptop 2006 13-inch screen……. and i lost my login password plus i lost my startup disc to…. it is anyone there can probably know what to do please help me i do not what to do thank you very much
Do you know how to disable the verbose mode definetely? I have activated it on a mb late 2008, and now I cannot disable it anymore… how can I do that?
thanks
Kind Regards
gp
sudo nvram boot-args=””
or sudo nvram boot-args=
[…] Zdroj: OSXDaily […]
[…] Always boot Mac OS X in Verbose Mode – OS X Daily (tags: mac boot verbose osx computer howto bash apple) […]
[…] Want to always start in Verbose mode? Check out this article […]
[…] (Taken from an OSXDaily article.) […]
For those who want to exercise geekdom without satiating their true inner geek, you can do this and a lot of other stuff using a gui util like OnyX. But this is, of course, “funner.”
I would rather just hit command-v when necessary, I prefer the bells & whistles of a nice spunky graphic splash to some scrolling greek text