Rebuild the Mailbox & Reindex Messages to Fix Common Problems in Mail App for Mac OS X
![]() The Mail app bundled with Mac OS X is an excellent email client, but if you have a giant mailbox that has been in use for a long time you may encounter some peculiar problems with sluggishness, message content issues, and searching irregularities. Usually these issues are of distinct types; search errors where some messages don’t come up in results when you know they should, unusually slow behavior when performing mail searches, or just general mail content problems, where an opened message appears blank, incomplete, corrupt, or is otherwise displayed improperly.
The Mail app bundled with Mac OS X is an excellent email client, but if you have a giant mailbox that has been in use for a long time you may encounter some peculiar problems with sluggishness, message content issues, and searching irregularities. Usually these issues are of distinct types; search errors where some messages don’t come up in results when you know they should, unusually slow behavior when performing mail searches, or just general mail content problems, where an opened message appears blank, incomplete, corrupt, or is otherwise displayed improperly.
Fortunately these issues are very easy to correct thanks to a two step process of forcibly rebuilding the mailbox, and then forcibly reindexing all messages contained within the Mac OS Mail app.
Before proceeding, you may wish to consider clearing out the Spam/Junk mail folders contained in Mail app to help speed up both reindexing and rebuilding. Such junkmail housekeeping can become automated with a simple settings adjustment as described in this collection of great tips for Mac Mail.
Rebuilding the Mailbox in Mail
Rebuilding a mailbox in Mail for Mac is very simple:
- Launch Mail app if you have not done so already
- Pull down the Mailbox menu, then choose “Rebuild”
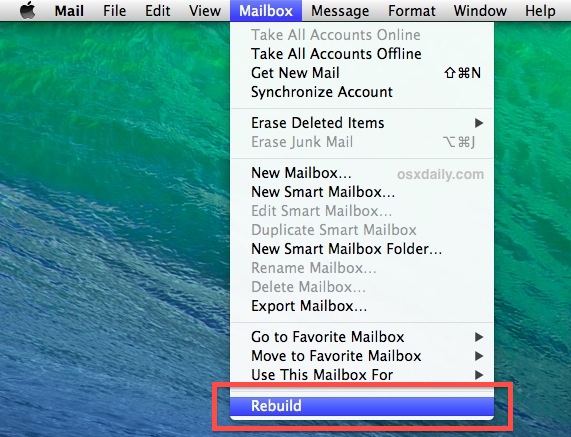
(If you don’t see the Rebuild option or it is greyed out, close any compose windows and select the inbox in the primary Mail app window)
This rebuild process can take a few minutes, or even an hour or more depending on how large your inbox and sent messages folders are.
An important note: this may cause significant bandwidth use for mailboxes configured with IMAP or Exchange, because the locally stored messages are removed and then redownloaded from the remote mail server. That can make this task unsuitable for users who are connected to the internet using a data capped connection, like a smartphone with hotspot.
Repair & Reindex All Messages in Mail app on Mac
You may encounter an alert from Mail app telling you that the mailbox must be repaired, but you can also do this manually. This is particularly helpful if the search functions of the Mail app have become unreliable.
- Quit out of Mail app and go to the Finder
- Hit Command+Shift+G and go to the following path:
- Open the latest V# folder (V9, V8, V7, V6, V4 etc), then open the “MailData” folder in that directory
- Delete every file that begins with “Envelope Index” (optional but recommended: back up these files to the desktop just in case something goes awry)
- Close the MailData window, then relaunch Mail app to force reindexing
~/Library/Mail/

Like rebuilding the mailbox, the reindexing process can also take a while, depending on how large the mailbox is and how much mail is stored on the computer. Be prepared for a lengthy re-indexation if you have tons (thousands+) of messages in Mail app. When finished, try the search or perform the task that you had issues with before and things should be working as usual again.
–
These two solutions will fix most common mailbox related issues encountered in Mail for Mac, so try them out the next time Mail app is performing strangely.
On the mobile side of things, iOS does not have similar forced rebuilding and reindexing options, and thus to resolve similar issues you often have to remove the account from iOS / iPadOS Mail settings and then re-add it to resolve like problems, but that’s a topic for another article entirely.


After deleting the ‘Envelope’ things I restart Mail, it takes hours to import all mails again and at the very end Mail gives an error… very frustrating… when I check the V folder again, I see that some of the ‘Envelope’ things came back in the V folder,
what should I do?
i just want to repeat what lots of other have written.
I rooted around all afternoon for a solution to the fact that MAIL crashed & would not open. In more attempts than were rational MAIL opens an crashed within seconds.
Following your instructions
& copying your command
fixed it.
There is nothing more to say
other than THANK YOU….jt
Just wanted to thank whoever wrote this post.
You saved my mail!
Although in Mojave “V6/Maildata” is the new “V2/Maildata”, the encantation for reindexing (deleting the “Envelope Index*” files) still works.
Mail in High Sierra (10.13.4) is a little different, as there is a V2 and a V5 folder. The MailData folder is in V5.
I have both Flag and Smart Mailbox problems. I have about 30,000 messages equally divided between iCloud and “On My Mac”. All my messages display properly in their respective mailboxes, and all their colored Tags show up too. However, none of these Flags are counted, and there are no messages in my numerous Smart Mailboxes!
The above problems appeared after I restored the previously “corrupted” Mailbox folder with a backup that worked perfectly in an identical computer. Any suggestions?
When I tried deleting the “Enveloper Index…” files for Mail 9.3 in OS X 10.11 El Capitan, all messages (IMAP) are re-downloaded. That’s hundreds of thousands of messages.
I think a mailbox rebuild might have been equally useful. My problem was that Mail couldn’t find messages when searching in Mail, though Spotlight searches did find them. Very irritating.
===Mail Crash Repeatedly===
ErrorMsg:
***terminating app due to exception while holding database lock ‘nsinvalidargumentexception’, reason: ‘*** -[__nssetm addobject:]: object cannot be nil
Issue solved with the solution “rebuilding Mailbox”. Only to kill three index files and goes to rebuild Mailbox then work again as usual.
THANKS A MILLION.
After a system update a couple of days ago, all my subfolders disappeared. If I search by folder name, emails in the folder display, but only a fraction of the messages that should be there. If I click on the “On My Mac” Show button, I’m asked to name a new mailbox. None of the old boxes show. If I create a new mailbox, it doesn’t display either.
Help! I’m using “El Crapitan,” version 10.11. Has anyone else had this problem? If so, does the rebuild/reindex process work? The simple fixes I’ve found online don’t work, by the way.
Worked fine for me.
However, after a few weeks the problem resurfaced when I tried to drag/drop a message from one mail account to another instead of emailing it.
Worked for me fine.
However, the problem resurfaced after a few weeks when I tried to drag/drop a message from one mail account to another instead of emailing it.
Re-indexed done with no problem as per your instructions, but The problem is 9 out of my 10 mailboxes have been restored but the main mail box which was the largest, the mailboxes show on mail app but they have no e-mail inside. I get a gray “no message selected” message in the main box of the viewer window.
I can send mail & the recipent also receives it, I just can’t see it! Is there a proper fix for this yet?? please advice
i also tried deleting the Gmail id mailbox which i could not see & then tried to setup the same again from start but the app keeps giving me the error that “this account already exists” or ” duplicate account” and dose not allow me to proceed… please advice
Many thanks…
Sandeep
Thanks that worked for my Mail! Just a small suggestion, It may not find any files on v2, but in the syntax if you change it to v3, it may work. I worked for me. So find out how your mail files are named.
Thank you so much. This completely fixed my issue. Nice to find information that works!
I’m getting a message saying “folder can’t be found”.
As it turns out, the “V2” in this link should be “V3” instead, thus:
~/Library/Mail/V3/MailData/
Both options did not do the trick. Problems remain, i.e. can not rename , re-move or delete (some) folders in Mail (osx 10.6.8)
The second suggestion (deleting envelope-files) when searching for ~/Library/Mail/V2/MailData/, it turned out that I do not have such folder on my system at all ???????
Hi all, mine is a very specific issue – I am not sure if it is a bug or if it just the way that Mail in El Capitan is set up to work.. but i hop not as i really miss this feature!
I have lots of folders and subfolders for my emails .. and I have always used this feature: – where you do a search and find an email, and then in the top right it tells you what folder that email is – and it is an active link.. you can click on that and that mailbox will open.
This has always been the way it works.
Now – with El Capitan.. I have noticed that with new emails I create and put in a folder.. in searches when these emails are found that link to show the containing folder is not there at all..
.. and with the emails that I imported from my previous OS system.. it does show the folder that this email lives in.. but it is not a link..
But I don’t think this is a rebuilding mailbox issue, because all my (MANY) emails are there … rather it seems like this is just the behaviors of El Capitan?? Which would be very strange and disappointing because it was such an important useful feature.
If any knows hope to get this functionality back I would be soo grateful! :-)
non worked; so rebuilt as described, now İ just have some 250 emails in the incoming po.box, thousands of the rest being lost, the “offline” issue for sending e mail remains. Any ideas?
Thank you. Worked for me (El Capitain) but Mail has been very buggy for months. I wish Apple had the decency to fix it themselves instead of leaving it to others!
If you’re repairing Mail in El Capitan, the “Envelope Index” files are in:
~/Library/Mail/V3/MailData/
The folder V2 is no longer used.
tnx! the manual envelop index removal tip worked for me.
Tnx again!
Just installed Thunderbird on the Mac. 4 minutes later, the connect is done.
The mail app is a piece of crap. Did all as per the excellent recommendations, nada. The app continually drops passwords, something Thunderbird NEVER does on windows. This is simply unacceptable, a situation that has gone on FOR years. Will try to find something else to eliminate this sorry problem.
I went through hours of pain to fix mail after the El Capitan debacle. Now today they release (Oct 26) an update to mail and once again my mail is screwed. Apple is getting brutally bad.
Same issue. No mail. Very UPSET!
I am having the same problem – the search function will not work on my mail after upgrading to El Capitan. I tried re-indexing my mail via Spotlight with no luck. I re-built every one of my 100+ mailboxes, still did not work. When I tried manually re-indexing by using the following method:
Quit out of Mail app and go to the Finder
Hit Command+Shift+G and go to the following path:
~/Library/Mail/V2/MailData/
Delete every file that begins with “Envelope Index” (optional but recommended: back up these files to the desktop just in case something goes awry)
Close the MailData window, then relaunch Mail app to force reindexing
Unfortunately, my MailData file contains only one file (Accounts.plist), so this does not work, either. I use the search function a lot, so any suggestions in fixing this would be greatly appreciated.
I have the exact same problem with the search function.
There is no material online so far how to solve this problem!
Awesome!! worked as charm, I tried other “solutions” even reinstall OS, You guys from OSXDaily really rock!
tried this solution, but when I saw the time to complete time reach 124 hours I cancelled it…. lol
too funny!
Tried everything that was recommended on this site and others and search still doesn’t work. Go figure.
me too… how long even IS that (ok don’t answer)… the “time to rebuild” just kept rising so i quit. Now what! Agh!!
Hey Jeff, if ur still stuck, i FINALLY got this working. I realised it kept getting up to ‘import #674’ then hanging… hence the ‘time remaining’ blowing out to weeks. Solution? I got brutal and deleted not just plist files and all those preference-related thingies, but the ENTIRE CONTENTS of my V2 and V3 folders (well… moved them to a temp folder just in case).
Fearing the worst, i restarted Mail, and after it looking a little bit lost, it suddenly came up and showed me all my old accounts (mainly pop3, but one from gmail) and hey hey, it SEEMS to be all working again! Woo hoo! Only wiped out my entire morning! Thankfully it’s a public holiday today :-))
Sure… i was prepared to lose all my old emails (i know i can search *within* the old email files I’ve moved to elsewhere if i’m really keen down the track), so it just has current emails still stored on whatever cloud in server-land, but this is a major breakthrough.
I can USE Mail again!
Was seriously looking at moving over to Outlook or something (until i heard El Capitan was having bugs with *that* too!
Jeff,
Keep watching; mine initially said 124 hours but within a minute had reduced the estimate to 7 minutes, which turned out to be accurate.
Iam running El Capitan and have been having problems with Mail
I am trying your fix above and I ‘assume’ (dangerous, I know), that the file path to the Envelope files you reference above are, under El Capitan:
/Users/username/Library/Mail/V3/MailData/
Did this work? I am having the same problem, but am afraid to “assume” V3 is the right path in El Capitan.
I tried it on El Capitan with no results.
Updated El Capitan on iMac a couple of says ago and yesterday upgraded iPhone to latest version of OSX. This morning I came in and my Exchange email has disappeared in the From drop down and been replaced by the email address I use for my Google calendar. I am doing a rebuild as suggested above, but the in the “Account Info” Summary box the Account description is Exchange, my full name appears as does my User Name but the Email address section is blank!!
Any idea what is going on? Will the rebuild solve the problem. Already lost 2 hours trying to find the answer to my problem on Apple site. No dice until I came across your suggestions on OSXDaily.com. Hoping you can shed some light on why my main email address on Exchange has been hijacked by my Google calendar address which I never use for emails? Doh! Feeling frustrated and bemused.
Marcus
When I try to delete envelope index files it shows that operation can’t be completed because the item “envelope index” is in use. What do I do??? Have been google-searching the answer all day.
What’s an envelope index file? This is about rebuilding a mailbox and reindexing your messages in Mail app, so if you want to do those this detailed walkthrough shows that, but an envelope? Not sure what you mean.
One point in the instructions(under title “Repair & Reindex All Messages in Mail app”) is: “Delete every file that begins with “Envelope Index” (optional but recommended: back up these files to the desktop just in case something goes awry)”
I can’t delete them because when you press empty trash it says “operation can’t be completed because the item “envelope index” is in use”
Quit Mail before trying to delete the Envelope Index files.
Thanks for these tips, i use an ancient version of OS X and i had some troubles with blank messages.
The 10.10.4 OSX update fixed my problem of Mail not opening multiple emails when a group was double-clicked.
Thank you so very much for this. It actually fixed the strange problems I started having in Mail. The verizon sub-email still isn’t working so I’m going to look around your site for a fix for that too.
The Mail search function suddenly stopped working at all today.
I did both delete envelop files and Rebuild but the problem remains!
Can anyone help me out?
Thanks!!!
Re-indexed with no problem as per your instructions, but The problem remains with Yosemite: the mailboxes show on mail app but they have no e-mail inside. I get a gray “no message selected” message in the main box of the viewer window.
I can send and receive mail, I just can’t see it! Is there a proper fix for this yet??
Many thanks…
Sandy
Hi Sandy
I don’t know if your problem is the same but I was having the same issue. Did all the steps yet still the same problem. Then I thought why not try to reorganize the view of the window? I suddenly remembered the small line that separates the list from the message. It was stuck at the top. I hovered over it to grab the line and pulled it down. There were all my messages! Argh! So simple I felt so stupid! Maybe this help you.
OK, it appears that what happens is:
*ForceQuit and Activity monitor say Mail not responding.
*After a long time, the three Envelope Index files in ~Library/Mail/V2/MailData ultimately stop changing and Activity Monitor stops showing any CPU use
*Then one needs to force quit Mail and restart it. Perhaps more than once (It took me 3 times.)
*Then there is a new and accurate index and Mail is noticeably faster.
P
I am currently trying to re-index with the instructions here. I get the expected ‘preparing to import messages’ message, and I am expecting it to take a very long time, as I have too many mailboxes and too much mail.
My question is: Should Force Quit say Mail is not responding during this? Activity Monitor says Mail is not responding but also shows changes in % CPU time, and threads, which suggests that something is happening and that I should simply be patient – that the ‘not responding’ is what I should expect to see while Mail is re-indexing.
Confirmation that this is expected would make my day better….
P
Worked for me. Thanks! Just recovered thousands of e-mails that had disappeared from the “On My Mac” folder that was holding them.
Reindexing fixed the problem of bogus numbers in my Flagged Mail folder. Now however, I cannot open more than one email at a time no matter which folder I choose.
Advice?
Thanks,
Steve
Clarification: double-clicking when multiple emails are selected does not open any of them. However, cmd-o does…
Steve
I have a corrupted Envelope Index file and cannot backup my iMAC (SuperDuper stops when it come to that file). Cannot copy the file either to another drive, only move to Trash
When I move the Envelope Index and the two other Envelope Index files to Trash and then restart Mail (osx 10.9.5), it asks if I wish to implement a new MAIL and to import my old mails.
Is this what the previous correspondents did to recreate the indexes, or am I missing something ? I really don’t want to lose my mails,
thanks for your advice,
Stuart
Stuart,
Yes, tell Mail to go ahead and import the old emails. It’s just a slightly misleading message; what will go on behind the scenes is it will re-create the Envelope Index files.
Thanks for this one. Had many of the symptoms (Yosemite) and have an enormous amount of email so was reluctant to do a rebuild that would re-download all data.
Tried the reindexing and wow! Lingering fetch processes are now gone and everything is much snappier. I suspect my searches will now be more accurate too. Based on my experience, I’d recommend this (second step, reindexing) to anyone looking to pep up their Mail. Only took about 10 minutes to reindex something like 140,000 emails.
Gratitude.
perfect. apple mail works again. thank you!!!
Oh I spoke too soon, the crashes are back–it must be something that gets back into your program as you use mail
The second fix –reindexing (deleting the envelop files) using the library stopped mac mail from crashing after a Yosemite install–I had 70,000 messages stored in IMAP
This fix seems to have worked for me (MacBook Air, Yosemite), thank you. It was driving me mad!!
Hi, I have recently installed Yosemite from scratch. I used to have some old e-mail on my Mac not on the server and I backup them by copying the folder ~/Library/Mail/V2/Mailboxes witch had a series of files like e-mails 2009.mbox
I did the clean install and the I’ve copied the contents of the backup to the ~/Library/Mail/V2/Mailboxes on the new install.
The problem is that the mailboxes show on mail app but they have no e-mail inside.
After this I’ve tried to import the mailboxes to mail. The process finishes very quickly with no errors, but no mail shows on mail app.
Please help, I really need this e-mail back.
i have the same issue as Nivaldo, can someone help .
Same problem. I upgraded to Yosemite, and found some mail messages’s index are incorrect. Then I rebuild the mail box. But the rebuild never ends, and even I copy back the mail box from my time machine backups. The mail never show on Mail.app.
Some body help.
I’m a bit baffled here because I can’t find the MailDAta folder – I just get a not found message – running 10.6.8 – could that be it?
I have noticed the same problem. I follow the steps laid out and cannot seem to get any of it to work. What has to happen that is not discussed in the approach above?
Thank you for listing the manual option in deleting the “Envelope” files. This was particularly helpful today as Mail froze while loading in Yosemite (Mac OS X 10.10) and wouldn’t launch after a force quit.
I have tried your ‘fix’ of deleting files beginning with Envelope to rebuild and re-index my mail but the problem I have discovered remains.
Some of my local mailboxes are displaying the title and date received but the content therein is blank; I stress that only some of my mailboxes are affected not all – which I find really strange.
I am sure this has only arisen since my upgrade to Mavericks.
Same issue as Paul – after moving email to a different mailbox some are fine others lose all content. Tried both fixes to no avail. As an aside the “rebuild” function seems to do nothing – when I select it nothing happens at all.