Instantly Eject All Mounted Drives & Disks from the Command Line in Mac OS X
The next time you’re at the command line and need to eject every single mounted volume, hard drive, disk, disk image, and/or external drive attached to a Mac, you can instantly eject them all in one fell swoop with a handy osascript command string. This is great if you work frequently in the Terminal and you’re wanting to quickly pack up a workstation and head out, but it’s also very useful for remotely managing Macs through an ssh connection, or adding to a shell script, amongst other potential uses.
For those who are unfamiliar with osascript, it’s a command line interface to AppleScript that allows you to execute AppleScripts and OSA language scripts from the terminal. The functionality is quite simple, you basically just feed it a script or statement that you’d otherwise place into the AppleScript Editor, and the whole thing is handled from the terminal rather than having to launch into the GUI app within OS X. Let’s use osascript to eject all the mounted volumes on a Mac.
Ejecting All Mounted Volumes, Drives, and Disk Images via Terminal
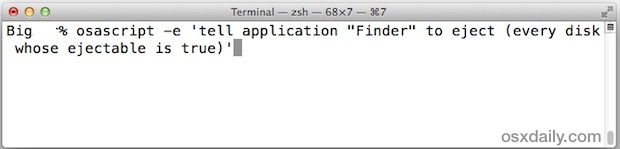
From the Terminal, run the following command string on a single line:
osascript -e 'tell application "Finder" to eject (every disk whose ejectable is true)'
As usual with the command line, be sure the entire command syntax is on one line. Unless your terminal window is set very large it will likely wrap, that’s ok.
The moment you hit the enter key to run the command, volumes will start ejecting. Disk images and network volumes go immediately, while external spinning hard drives will spin up first before ejecting. Nonetheless, even if you have to wait for the spin up of some drives the entire task is very fast and there is no further interaction required.
There are certainly other ways to do this, including with the hdiutil and diskutil tools, but the osascript method is probably the fastest since it ejects everything without having to use mount points. If you happen to know of another method to mass eject volumes, perhaps one that is cross platform compatible so that it’d work in Mac OS X as well as linux, do let us know in the comments.
Find yourself using this often? Consider adding it to your bash_profile with an alias to shorten the length of the command. Simply append something like the following to .bash_profile for this purpose:
alias ejectall='osascript -e 'tell application "Finder" to eject (every disk whose ejectable is true)''
This allows you only have to type ‘ejectall’ rather than the entire command string.
Of course, this is all a bit advanced, and most Mac users are better served ejecting disks by holding down the eject key, or going through the OS X Finder by finding them in the sidebar, hovering over the name, and clicking the eject button.
In Mojave I was not able to get any of these to work as a .profile alias.
I did manage to get ejectall working by placing the command in a script file and calling that from an alias.
~/ejectall.sh conatins:
#!/bin/sh
osascript -e ‘tell application “Finder” to eject (every disk whose ejectable is true)’
.profile contains:
alias ejectall=’~/ejectall.sh’
Finally, flag ejectall.sh as executable:
chmod 755 ~/ejectall.sh
is there a command or script to eject all mounted drives on shutdown?? or log out?
i have this problem in yoesemite, if i forgot to eject the drives it won’t shutdown, it looks that is shutting down but it stops on a black screen with the pointer still visible.
Is there a way to do this but not eject certain drives?
Worked perfect for me but I didn’t use terminal. Instead I created a Service script with Automator and added the exact command you posted to it. Now I have a hot key that I press and all my devices and multivolume devices eject. You are the best! Thank you. I’m on El Capitan Macbook Pro. I’m also going to write up how I did it on my blog. Thank you again. One last thing. Can you post a command to Mount all volumes?
With Yosemite, you have to hold down the “Option” key if any of the mounted volumes are partitioned.
This also works:
alias eject=`osascript -e ‘tell application “Finder” to eject (every disk whose ejectable is true)’`
I just select the icons of the volumes on my desktop and type “command + E”, holding it until the volumes are ejected.
So simple…
I use a little program called Semulov (“volumes” backward). In the menu bar, it lets me eject all or one specific volume.
alias ejectall=’osascript -e “tell application \”Finder\” to eject (every disk whose ejectable is true)”‘
I did the following from Terminal:
#Make a new shell script called ejectall.sh in the same directory as the .bash_profile
nano ejectall.sh
#Added the following
osascript -e ‘tell application “Finder” to eject (every disk whose ejectable is true)’
#Hit control + o to save and control + x to quit nano
#Make ejectall.sh executable by running the following
chmod +x ejectall.sh
Then in the .bash_profile add the following
alias ejectall=’./ejectall.sh’
#control + o to save and control + x to quit
#Restart terminal.
Nope, still doesn’t work. Anyone using this successfully? Please copy and paste your command here so I can copy. Why does it also say “command not found”? I’ve tried some simple aliases and still get the same error message. Path question?
Or this:
alias ejectall=”osascript -e ‘tell application “Finder” to eject (every disk whose ejectable is true)'”
What version of OS X are you using? Try typing ‘osascript -blah’ and see if you get an illegal option response
10.9.3
The encoding in stan-o’s solution may not work, depending on your shell/OS.
alias ejectall=’osascript -e ‘”‘”‘tell application “Finder” to eject (every disk whose ejectable is true)'”‘”
^ works for me (OSX 10.8.5, Terminal)
Keep in mind, if you edit any of your .bash_* files, you have to restart your terminal session before the changes will take effect — i.e., open a new terminal tab, or quit/reopen terminal.
Neither of these works for me. I only get “command not found” as a result. Is there a path setting I have to change? And does it matter if the single and double quotation marks are straight or fancy? Terminal novice here.
The quotations must be straight quotes not curly or fancy. Try just copying and pasting the command as seen on the page, that should do it.
Your alias code is invalid, here’s the one that works:
alias ejectall=’osascript -e ‘”‘”‘tell application “Finder” to eject (every disk whose ejectable is true)'”‘””